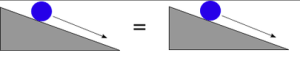The Female Mathematician Who Changed the Course of Physics-But Couldn't Get a Job

By 1915, any list of the world’s greatest living mathematicians included the name David Hilbert. And though Hilbert previously devoted his career to logic and pure mathematics, he, like many other critical thinkers at the time, eventually became obsessed with a bit of theoretical physics.
With World War I raging on throughout Europe, Hilbert could be found sitting in his office at the great university at Göttingen trying and trying again to understand one idea—Einstein’s new theory of gravity.

Göttingen served as the center of mathematics for the Western world by this point, and Hilbert stood as one of its most notorious thinkers. He was a prominent leader for the minority of mathematicians who preferred a symbolic, axiomatic development in contrast to a more concrete style that emphasized the construction of particular solutions. Many of his peers recoiled from these modern methods, one even calling them “theology.” But Hilbert eventually won over most critics through the power and fruitfulness of his research.
For Hilbert, his rigorous approach to mathematics stood out quite a bit from the common practice of scientists, causing him some consternation. “Physics is much too hard for physicists,” he famously quipped. So wanting to know more, he invited Einstein to Göttingen to lecture about gravity for a week.
Before the year ended, both men would submit papers deriving the complete equations of general relativity. But naturally, the papers differed entirely when it came to their methods. When it came to Einstein’s theory, Hilbert and his Göttingen colleagues simply couldn’t wrap their minds around a peculiarity having to do with energy. All other physical theories—including electromagnetism, hydrodynamics, and the classical theory of gravity—obeyed local energy conservation. With Einstein's theory, one of the many paradoxical consequences of this failure of energy conservation was that an object could speed up as it lost energy by emitting gravity waves, whereas clearly it should slow down.
Unable to make progress, Hilbert turned to the only person he believed might have the specialized knowledge and insight to help. This would-be-savior wasn’t even allowed to be a student at Göttingen once upon a time, but Hilbert had long become a fan of this mathematician’s highly "abstract" approach (which Hilbert considered similar to his own style). He managed to recruit this soon-to-be partner to Göttingen about the same time Einstein showed up.
And that’s when a woman—one Emmy Noether—created what may be the most important single theoretical result in modern physics.
Emmy who?
Emmy (officially Amalie Emmy) Noether, born 1882, did not stand out in any particular way as a child, although she did, on occasion, attract some notice for her astonishing quickness in providing accurate answers to puzzles or problems in logic or mathematics. Her father, Max, was a fairly prominent mathematician, and one of her brothers eventually attained a doctorate in math. In retrospect, perhaps the Noethers may be another historical example of a family with a math gene.
Germany in the early years of the 20th century was not a convenient place for a woman who wanted to pursue mathematics, or for that matter, any academic field outside of a few considered appropriate for the sex. Luckily for Noether, she had a facility with languages and was allowed to become certified as a language teacher. But Noether recognized her passion was in mathematics, and she decided to chase her dream and find a way to study the subject at the university level.

While women were not permitted to be official students at most German universities then, they were able to audit courses with the permission of the professor. Noether started this way, sitting in on classes at the University of Erlangen. But she also spent a semester in 1903−1904 auditing courses at Göttingen, where she first encountered Hilbert. Rules surrounding enrollment eventually relaxed, and Noether later matriculated at Erlangen to earn her doctorate in mathematics (summa cum laude) in 1907.
However, women were still not accepted as teachers in German universities at the time. Emmy took her fresh doctorate and became an unofficial assistant to her ailing and increasingly frail father, a professor at Erlangen. She also vigorously attacked her own research, forging a personal and original path through abstract algebra. Just a year after her doctorate, Noether's papers and the doctoral research that she was unofficially supervising gained her election to several academic societies, which prompted invitations to speak around Europe. Among those wanting her around, Hilbert reached out to bring Noether to Göttingen in order to tackle Einstein’s theory.
The problem with Einstein’s theory
No one denied it—Einstein’s Theory of General Relativity was undoubtedly beautiful. It was unlike any theory of nature yet imagined by humankind, more surprising and radical even than the special theory of relativity that Einstein had laid out in his revolutionary paper ten years before.
Newton described gravity simply as a force acting over a distance attracting any two masses, whether planets or apples, to each other. The force was proportional to the product of the two masses and inversely proportional to the square of the distance between them. That’s the entire story, and it worked well for over two hundred years.
But there was a mystery embedded in this description of gravity that physicists lived with for those two centuries. This coincidence was impossible to ignore, yet seemingly impossible to explain. The mass that determined the strength of the gravitational force was the same mass that appeared in Newton’s second law of motion, F = ma; gravitational mass was the same as the “inertial mass.” There was no apparent reason this had to be true, it simply was.
Einstein didn’t think this was mere coincidence. He formulated a “principle of equivalence” that can be described in several ways. One way is to insist that the two types of mass are identical because of a fundamental symmetry in nature; that the laws of physics must take the same form whether one is in a gravitational field or in a region of space with no gravity (say, in a spaceship undergoing an equivalent acceleration). Carrying this principle to its logical conclusions eventually led to the equations of general relativity, the theory considered by many (including the great theoretical physicist Lev Landau) to be “probably the most beautiful of all existing physical theories.”
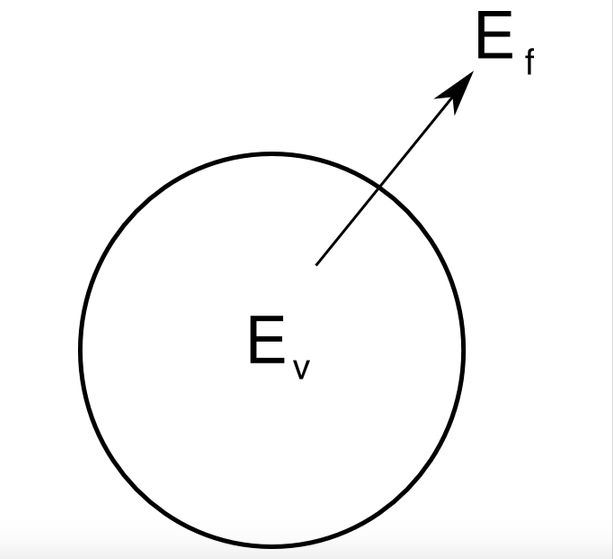
Although Hilbert recognized that general relativity was a tremendous accomplishment, the energy conservation conundrum struck him as unacceptable. To illustrate this idea, let’s draw a circle around a region of space, as in the diagram here.
The circle might contain electric and magnetic fields, water in motion, or something else. If we keep track of the energy flowing out of (and into) the perimeter of the circle (Ef) during a certain interval of time, then that total transfer of energy is equal to the amount that the total energy inside the circle (Ev) has changed. This is local energy conservation. In simple terms, energy is not created or destroyed, just moved around.
Listing image by Flickr user: Eli Brody
Noether's Theorem
During Noether’s stay at Göttingen, Hilbert contrived a way to allow her to lecture unofficially. He repeatedly attempted to get her hired as a Privatdozent, or an officially recognized lecturer. The science and mathematics faculty was generally in favor of this, but Hilbert could not overcome the resistance of the humanities professors, who simply could not stomach the idea of a female teacher. At one meeting of the faculty senate, frustrated again in his attempts to get Noether a job, he famously remarked, “I do not see that the sex of a candidate is an argument against her admission as Privatdozent. After all, we are a university, not a bathing establishment.”
Social barriers aside, Noether immediately grasped the problem with Einstein's theory. Over the course of three years, she not only solved it, but in doing so she proved a theorem that simultaneously reached back to the dawn of physics and pushed forward to the physics of today. Noether’s Theorem, as it is now called, lies at the heart of modern physics, unifying everything from the orbits of planets to the theories of elementary particles.
The full statement of Noether’s Theorem involves a good amount of advanced mathematics, far beyond the scope of this article. But it has a clear and intuitive physical meaning: the theorem uncovers a hidden relationship between symmetry and conservation, and that relationship is what came to unify all of physics.
To start, symmetry in a physics sense refers to whether you can change something about an object or a system and have everything look and behave the same. A sphere has a lot of symmetry, because you can change its orientation by rotating it around any axis by any angle, and it makes no difference. A cylinder has symmetry, but not as much as the sphere: it doesn’t change if you rotate it around its axis of symmetry, but if you rotate it around any other axis, it looks different. These are examples of continuous symmetries, because the angle can be as large or small as you like. A perfectly mirror-symmetrical butterfly is an example of a symmetry that is not continuous: you can reflect it around its midsection without changing its appearance, but there is no way to reflect it through different amounts.
A physics experiment gives the same result at different times. When something is immune to change in physics, it’s sometimes called invariant. The really important invariants in physics are transformations that leave the laws of physics themselves unchanged: so now we are talking about, instead of spheres and cylinders, whole systems of equations that describe how nature works. Time is an example. If the equations that describe the universe changed as time passed, we could never make sense of anything. We could do an experiment today and get one result, then try to repeat it in an hour and get something entirely different—even if nothing changed except the time that we made the measurements.
At a bare minimum, therefore, we require any theory in physics to be time invariant: we should be able to add a constant to the time variable wherever it appears in the equations and get the same equations back. Spatial invariance is another example. Physics should be the same no matter where in space we are, if nothing else changes. The equations of motion need to be the same in New York or Göttingen.
Spatial invariance in physics
These are also examples of continuous invariants, because we can shift time and space by an arbitrary amount. There are also discontinuous invariants, such as time-reversal, or mirror reflection. These also hold, at least in classical mechanics.
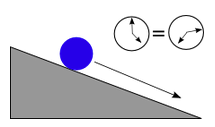
Noether’s Theorem relates continuous invariants to conservation laws. A conservation law is a rule that says that some quantity remains numerically constant as the system evolves in time. Conservation of energy, momentum, and angular momentum from classical physics are famous examples. Once you know a conservation law, you can often use it as a shortcut to solve problems. In the diagrams here, if the ball starts at rest at the top of the ramp and is allowed to roll down a certain distance under gravity, we can calculate its energy of motion (including its rotation) without having to figure out the force acting on it by using the law of conservation of energy.
In order to appreciate the astonishing power of the theorem discovered by Noether in 1918, we must fully understand the differences between conservation laws and invariants. Most of the elementary invariants are intuitively obvious, corresponding to our instincts about the structure of space and time. They reflect the fundamental symmetries of nature. (It would be strange if the very laws of physics altered themselves as we moved from place to place.) Conservation laws are not typically as obvious, often needing to be derived or discovered empirically. It may be hard to believe now, but conservation of energy was not discovered for almost 200 years after Newton published his laws of motion.
Noether’s Theorem proves that for every invariant, there is a corresponding conservation law. She also proved the converse, meaning that for every conservation law there must be an invariant behind it. (In this article we refer to “Noether’s Theorem” as physicists usually do and as is common in elementary discussions of the result. In fact, however, Noether proved four related theorems in the same paper: two theorems for invariants with different types of symmetry and their converses.)
The theorem shows that conservation of energy is equivalent to time invariance in classical physics. This hard-won yet essential conservation law is directly implied by, and implies, a fundamental symmetry of nature. It shows that momentum conservation is equivalent to spatial invariance. It establishes the equivalence of other symmetries, more mathematical in flavor, with other conservation laws. For example, the conservation of charge is related to a gauge symmetry, a complex mathematical symmetry in the equations of electrodynamics.
It is the theorem’s power to derive new conservation laws from abstract symmetries that has guided physical theory up to the present day. Noether’s result is an important tool in contemporary areas like particle physics, and it’s likely to remain so. But how did it solve the problem of energy conservation in general relativity?
Refer back to the diagram above, showing energy being carried out of a circular region, leaving a smaller amount of energy behind. In all the known theories of physics, including electromagnetism and Newtonian gravity, this energy could be carried by a body in motion, and the electric or gravitational field inside the circle could be considered part of an unchanging background, perhaps exerting a force on the body. Noether’s work helped shed light on the fact that Einstein’s gravity behaves as no theory devised before, in that the energy of matter moving in a gravitational field can not be considered separately from the energy of the field itself. There is a conservation law, but it involves taking all of matter and gravity in a region of space as a unified whole (the hairy mathematical details are laid out in §102 of this textbook).
In essence, Noether showed that Hilbert was correct—normal local energy conservation did not hold in Einstein’s work. However, she discovered that this was because of the peculiar kind of symmetry in general relativity. In this radically new model of the universe, gravity altered the very geometry of space and time. In a Euclidean world, the ratio of the circumference of a circle to its diameter equals π. But in Einstein’s universe, this ratio depends on where in space you happen to be.
Originally, Hilbert and his colleagues thought they had a problem: either general relativity was faulty or they had made a mistake. Noether showed them a new outcome. The Göttingen team did not make a mistake; energy conservation in general relativity just could not take the form that it had in all previous physics theories.

Untouched by it all
Long after she had earned it, Noether finally received the opportunity she wanted. Once the war ended and German politics and social attitudes underwent a rapid liberalization, Professor Noether lectured under Göttingen’s official auspices. While accounts seem to indicate classroom teaching wasn’t her strength, Noether proved to be a superb leader of small research groups. Her advanced students were devoted to her.
Sadly, this period would come to an end in 1933. The Nazis came to power, and Noether was not only female but Jewish. The Nazis’ purge of Jewish faculty in German universities had a particularly dramatic effect on the mathematical world. One-third of the mathematics professors, and three-fourths of the heads of Göttingen’s mathematics and physics institutes, were Jewish despite less than one percent of the German population identifying that way at the time.
With the help of other illustrious refugees who settled in the United States (such as Einstein), Noether ended up across the Atlantic in 1933. She soon settled into a visiting professor’s role at the venerable women’s college, Bryn Mawr, and had a very happy two years there. In 1935, however, Noether underwent an operation for an ovarian cyst and died of an infection within days at the age of 53.
Einstein, rather concerned that little notice of her death had been taken in the newspapers, wrote an obituary in the form of a letter that was published in The New York Times.
Emmy Noether, who, in spite of the efforts of the great Göttingen mathematician, Hilbert, never reached the academic standing due her in her own country, none the less surrounded herself with a group of students and investigators at Göttingen, who have already become distinguished as teachers and investigators.
But even if the public wasn’t aware of Noether’s greatness and passing, the mathematics community certainly was. Fellow Göttingen mathematics great Hermann Weyl delivered a moving eulogy at Noether’s funeral.
You did not believe in evil, indeed it never occurred to you that it could play a role in the affairs of man. in a sea of hate and violence, of fear and desperation and dejection — you went your own way, pondering the challenges of mathematics When you were not allowed to use the institute’s lecture halls you gathered your students in your own home. Even those in their brown shirts were welcome Many of us believed that an enmity had been unleashed in which there could be no pardon; but you remained untouched by it all.
In retrospect, Noether’s work seemed to unify the most abstract mathematics with the most basic physical intuition, unifying the earliest successful systems of physics with science yet unborn. The circumstances of her life provide a powerful example of the humanizing influence of science and mathematics. It was the exponents of these fields who were eager to welcome her into their fellowship without regard for her sex or ancestry; the men of philosophy, history, politics, and government sought to exclude her for these very reasons.
This year marks the 100th anniversary of the theory of general relativity, but Emmy Noether remains the tale’s best kept secret. Little by little, however, history seems to rediscover her brilliance. A street and school in her home town have been named after her, as well as a crater on the moon. And for her birthday on March 23, Google dedicated its coveted Doodle real estate to one of history's most under-appreciated minds.
Lee Phillips is a repeat features writer at Ars Technica. On a personal note regarding Noether’s work, he wrote: “I know I am not alone in my wonderment upon encountering the result while studying advanced classical mechanics as an undergraduate. Noether’s Theorem reveals the power of physics to provide a harmonious picture of nature at a more profound level than is possible without it. For me, this sealed the deal, dooming me to graduate school.”