Ever since the discovery of the bizarre behavior of quantum systems, we’ve been forced to reckon with a seemingly uncomfortable truth. For whatever reason, it appears that what we perceive of as reality — where objects are and what properties they possess — isn’t itself fundamentally determined. As long as you don’t measure or interact with your quantum system, it exists in an indeterminate state; we can only speak of the properties it possess and the outcomes of any potential measurements in a statistical, probabilistic sense.
But is that a fundamental limitation of nature, where there exists an inherent indeterminism until a measurement is made or a quantum interaction occurs? Or could there be a “hidden reality” that’s completely predictable, understandable, and deterministic underlying what we see? It’s a fascinating possibility, one that was preferred by no less a titanic figure than Albert Einstein. It’s also the question of Patreon supporter William Blair, who wants to know:
“Simon Kochen and Ernst Specker proved, purely by logical argument, that so-called hidden variables cannot exist in quantum mechanics. I looked this up, but [these articles] are beyond my... levels of math and physics. Could you enlighten us?”
Reality is a complicated thing, especially when it comes to quantum phenomena. Let’s start with the most famous example of quantum indeterminism: the Heisenberg uncertainty principle.
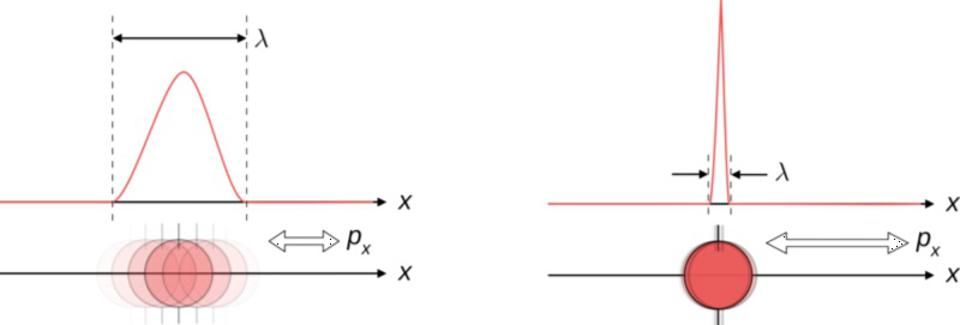
In the classical, macroscopic world, there’s no such thing as a measurement problem. If you take any object that you like — a jet, a car, a tennis ball, a pebble, or even a mote of dust — you can not only measure any of its properties that you want to, but based on the laws of physics that we know, we can extrapolate what those properties will be arbitrarily far into the future. All of Newton’s, Einstein’s, and Maxwell’s equations are fully deterministic; if you can tell me the locations and motions of every particle in your system or even your Universe, I can tell you precisely where they will be and how they’ll be moving at any point in the future. The only uncertainties we’ll have are set by the limits of the equipment we’re using to take our measurements.
But in the quantum world, this is no longer true. There is an inherent uncertainty to how well, simultaneously, you can know a wide variety of properties together. If you try to measure, for example a particle’s:
- position and momentum,
- energy and lifetime,
- spin in any two perpendicular directions,
- or its angular position and angular momentum,
you’ll find that there’s a limit to how well you can simultaneously know both quantities: the product of both of them can be no smaller than some fundamental value, proportional to Planck’s constant.
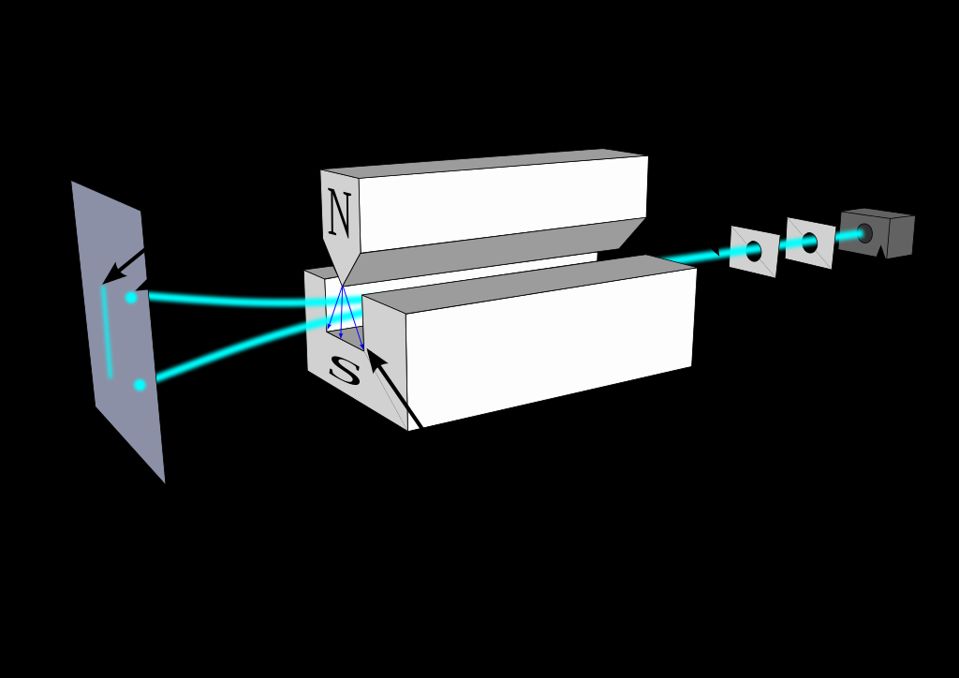
A beam of particles fired through a magnet could yield quantum-and-discrete (5) results for the particles' spin angular momentum, or, alternatively, classical-and-continuous (4) values. This experiment, known as the Stern-Gerlach experiment, demonstrated a number of important quantum phenomena. THERESA KNOTT / TATOUTE OF WIKIMEDIA COMMONS
In fact, the instant you measure one such quantity to a very fine precision, the uncertainty in the other, complementary one will spontaneously increase so that the product is always greater than a specific value. One illustration of this, shown above, is the Stern-Gerlach experiment. Quantum particles like electrons, protons, and atomic nuclei have an angular momentum inherent to them: something we call quantum “spin,” even though nothing is actually physically spinning about these particles. In the simplest case, these particles have a spin of ½, which can be oriented either positively (+½) or negatively (-½) in whatever direction you measure it.
Now, here’s where it gets bizarre. Let’s say I shoot these particles — in the original, they used silver atoms — through a magnetic field oriented in a certain direction. Half of the particles will get deflected in one direction (for the spin = +½ case) and half get deflected in the other (corresponding to the spin = -½ case). If you now pass these particles through another Stern-Gerlach apparatus oriented the same way, there will be no further splitting: the +½ particles and the -½ particles will “remember” which way they split.
But if you pass them through a magnetic field oriented perpendicular to the first, they’ll split once again in the positive and negative directions, as though there was still this uncertainty in which ones were +½ and which ones were -½ in this new direction. And now, if you go back to the original direction and apply another magnetic field, they’ll go back to splitting in the positive and negative directions again. Somehow, measuring their spins in the perpendicular direction didn’t just “determine” those spins, but somehow destroyed the information you previously knew about the original splitting direction.
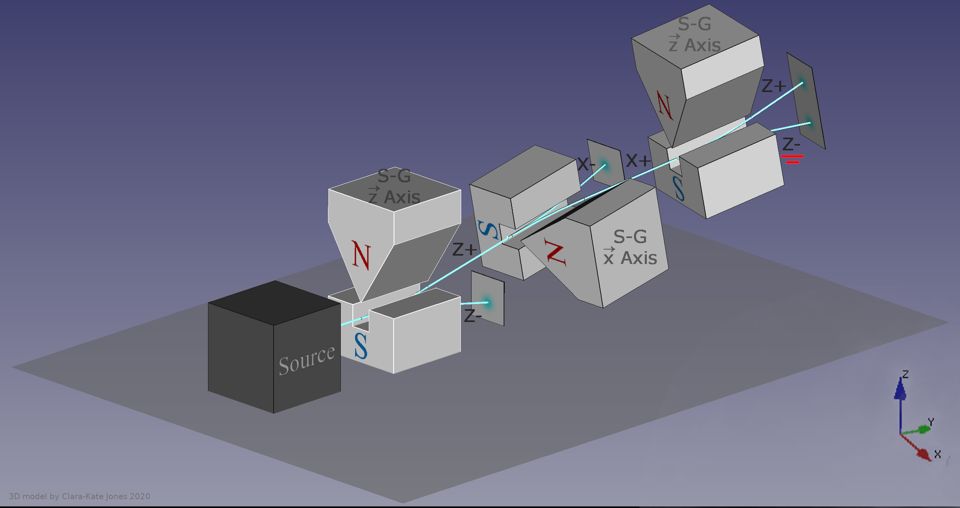
When you pass a set of particles through a single Stern-Gerlach magnet, they will deflect according to their spin. If you pass them through a second, perpendicular magnet, they'll split again in the new direction. If you then go back to the first direction with a third magnet, they'll once again split, proving that previously determined information was randomized by the most recent measurement. CLARA-KATE JONES/ MJASK OF WIKIMEDIA COMMONS
The way we conceive of this, traditionally, is to recognize that there’s an inherent indeterminism to the quantum world that can never be completely eliminated. When you exactly determine the spin of your particle in one dimension, the corresponding uncertainty in the perpendicular dimensions must become infinitely large to compensate, otherwise Heisenberg’s inequality would be violated. There’s no “cheating” the uncertainty principle; you can only obtain meaningful knowledge about the actual outcome of your system through measurements.
But there has long been an alternative thought as to what’s going on: the idea of hidden variables. In a hidden variables scenario, the Universe really is deterministic, and quanta have intrinsic properties that would enable us to predict precisely where they’d end up and what the outcome of any quantum experiment would be in advance, but some of the variables that govern the behavior of this system cannot be measured by us in our present reality. If we could, we’d understand that this “indeterminate” behavior that we observe is merely our own ignorance of what’s truly going on, but that if we could find, identify, and understand the behavior of these variables that truly underlie reality, the quantum Universe wouldn’t appear so mysterious after all.

Although, at the quantum level, reality appears to be jittery, indeterminate, and inherently uncertain, many have firmly believed that there may be properties that are invisible to us, but that nevertheless determine what an objective reality, independent of the observer, truly may be. We have not found any such evidence for this assertion as of 2021. NASA/CXC/M.WEISS
The way I’ve always conceived of hidden variables is to imagine the Universe, down at the quantum scales, to have some dynamics governing it that we do not understand, but whose effects we can observe. It’s like imagining our reality is hooked up to a vibrating plate at the bottom, and we can observe the grains of sand that lie atop the plate.
If all you can see are the grains of sand, it will look to you as though each individual one vibrates with a certain amount of inherent randomness to it, and that large-scale patterns or correlations might even exist between grains of sand. However, because you cannot observe or measure the vibrating plate beneath the grains, you cannot know the full set of dynamics that govern the system. Your knowledge is the thing that’s incomplete, and what appears to be random actually has an underlying explanation, albeit one that we do not fully understand.
This is a fun idea to explore, but like all things in our physical Universe, we must always confront our ideas with measurements, experiments, and observations from within our material Universe.

The results of the 'masked' double-slit experiment. Note that when the first slit (P1), the second slit (P2), or both slits (P12) are open, the pattern you see is very different depending on whether one or two slits are available. R. BACH ET AL., NEW JOURNAL OF PHYSICS, VOLUME 15, MARCH 2013
One such experiment — in my opinion, the most important experiment in all of quantum physics — is the double-slit experiment. When you take a even a single quantum particle and fire it at a double slit, you can measure, on a background screen, where that particle lands. If you do this over time, hundreds, thousands, or even millions of times, you’ll eventually be able to see what the pattern that emerges looks like.
Here’s where it gets weird, though.
- If you don’t measure which of the two slits the particle goes through, you get an interference pattern: spots where the particle is very likely to land, and spots in between where the particle’s very unlikely to land. Even if you send these particles through one-at-a-time, the interference effect still persists, as though each particle were interfering with itself.
- But if you do measure which slit each particle goes through — such as with a photon counter, a flag, or via any other mechanism — that interference pattern doesn’t show up. Instead, you just see two clumps: one corresponding to the particles that went through the first slit and the other corresponding to those that went through the second.
And, if we want to try and pin down what’s actually going on in the Universe even further, we can perform another type of experiment: a delayed-choice quantum experiment.
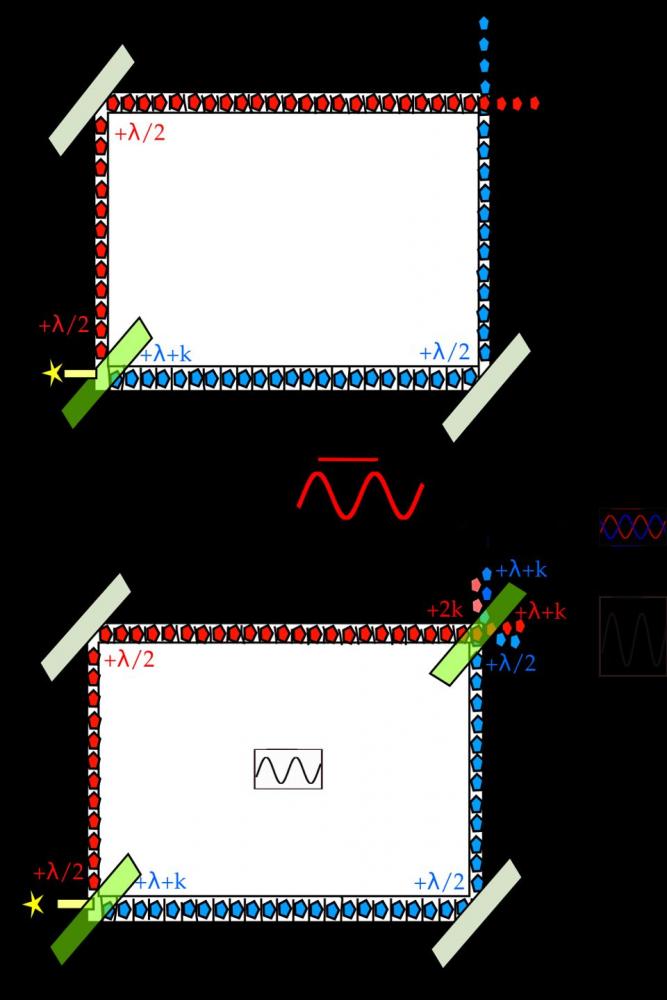
This image illustrates one of Wheeler's delayed-choice experiments. In the top version, a photon is sent through a beam splitter, where it will either take the red or the blue path, and hit one detector or the other. In the bottom version, a second beam splitter exists at the end, producing an interference pattern when the paths are combined. Delaying the choice of configuration has no effect on the experimental outcome. PATRICK EDWIN MORAN/ WIKIMEDIA COMMONS
One of the greatest physicists of the 20th century was John Wheeler. Wheeler was thinking about this quantum “weirdness,” about how these quanta sometimes behave as particles and sometimes as waves, when he began to devise experiments that attempted to catch these quanta acting like waves when we expect particle-like behavior and vice versa. Perhaps the most illustrative of these experiments is shown above: passing a photon through a beam splitter and into an interferometer, one with two possible configurations, “open” and “closed.”
Interferometers work by sending light in two different directions, and then recombining them at the end, producing an interference pattern dependent on the difference in the path lengths (or the light-travel time) between the two routes.
- If the configuration is "open" (top), you'll simply detect the two photons individually, and won't get a recombined interference pattern.
- If the configuration is "closed" (bottom), you'll see the wave-like effects on the screen.
What Wheeler wanted to know is if these photons "knew" how they'd have to behave in advance. He'd start the experiment in one configuration, and then, right before the photons arrived at the end of the experiment, would either "open" or "close" (or not) the apparatus at the end. If the light knew what it was going to do, you'd be able to catch it in the act of being a wave or particle, even when you switched the final outcome.

Trajectories of a particle in a box (also called an infinite square well) in classical mechanics (A) and quantum mechanics (B-F). In (A), the particle moves at constant velocity, bouncing back and forth. In (B-F), wavefunction solutions to the Time-Dependent Schrodinger Equation are shown for the same geometry and potential. The horizontal axis is position, the vertical axis is the real part (blue) or imaginary part (red) of the wavefunction. These stationary (B, C, D) and non-stationary (E, F) states only yield probabilities for the particle, rather than definitive answers for where it will be at a particular time. STEVE BYRNES / SBYRNES321 OF WIKIMEDIA COMMONS
In all cases, however, the quanta do exactly what you’d expect when they arrive. In the double slit experiments, if you interact with them as they’re passing through a slit, they behave as particles, while if you don’t, they behave as waves. In the delayed-choice experiment, if the final device to recombine the photons is present when they arrive, you get the wave-like interference pattern; if not, you just get the individual photons without interference. As Niels Bohr — Einstein’s great rival on the topic of uncertainty in quantum mechanics — correctly stated,
“...it...can make no difference, as regards observable effects obtainable by a definite experimental arrangement, whether our plans for constructing or handling the instruments are fixed beforehand or whether we prefer to postpone the completion of our planning until a later moment when the particle is already on its way from one instrument to another.”
But does this rule out the idea that there could be hidden variables governing the quantum Universe? Not exactly. But what it does do is place significant constraints on the nature of these hidden variables. As many have shown over the years, beginning with John Stewart Bell in 1964, if you try to save a “hidden variables” explanation for our quantum reality, something else significant has got to give.
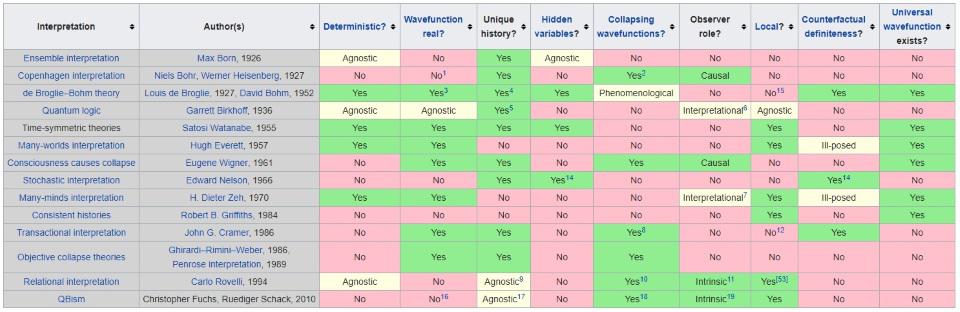
A variety of quantum interpretations and their differing assignments of a variety of properties. Despite their differences, there are no experiments known that can tell these various interpretations apart from one another, although certain interpretations, like those with local, real, deterministic hidden variables, can be ruled out. ENGLISH WIKIPEDIA PAGE ON INTERPRETATIONS OF QUANTUM MECHANICS
In physics, we have this idea of locality: that no signals can propagate faster than the speed of light, and that information can only be exchanged between two quanta at the speed of light or below. What Bell first showed was that, if you want to formulate a hidden variable theory of quantum mechanics that agreed with all of the experiments we’ve performed, that theory must be inherently nonlocal, and some information must be exchanged at speeds greater than the speed of light. Because of our experience with signals only being transmitted at finite speeds, it’s not so hard to accept that if we demand a “hidden variables” theory of quantum mechanics, locality is something we have to give up.
Well, what about the Kochen-Specker theorem, which came along just a few years after the original Bell’s theory? It states that you don’t just have to give up locality, but you have to give up what’s called quantum noncontextuality. In simple terms, it means that any experiment you perform that gives you a measured value for any quantum property of your system is not simply “revealing pre-existing values” that were already determined in advance.
Instead, when you measure a quantum observable, the values you obtain are dependent on what we call "the measurement context," which means the other observables that are measured simultaneously along with the one you're specifically after. The Kochen-Specker theorem was the first indication that quantum contextuality — that the measurement result of any observables depends on all the other observables within the system — is an inherent feature of quantum mechanics. In other words, you cannot assign values to the underlying physical quantities that are revealed by quantum experiments without destroying the relationships between them that are essential to the functioning of the quantum Universe.
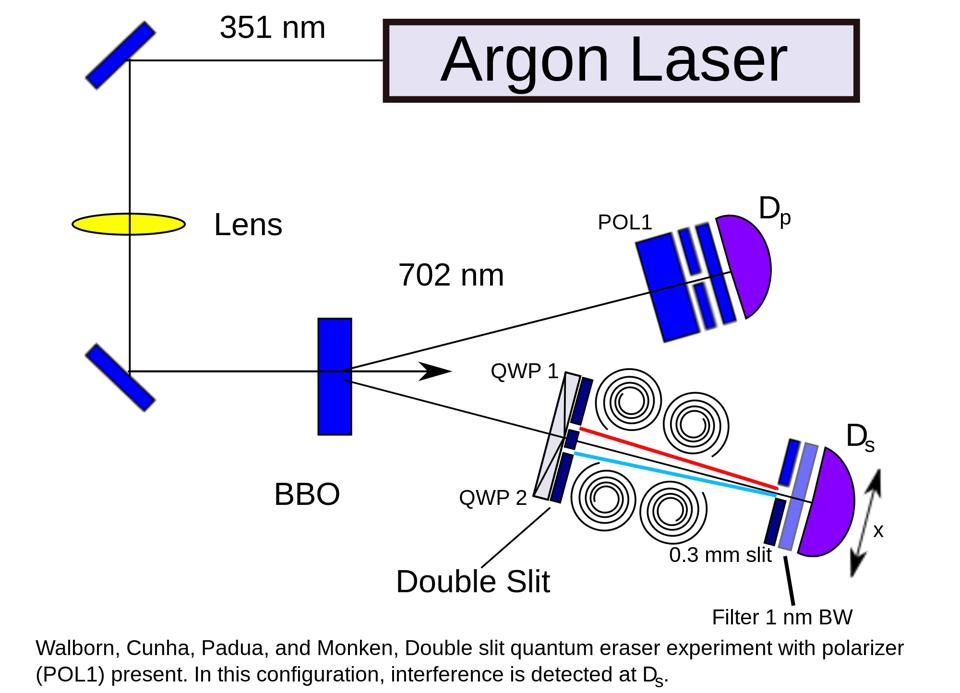
A quantum eraser experiment setup, where two entangled particles are separated and measured. No alterations of one particle at its destination affect the outcome of the other. You can combine principles like the quantum eraser with the double-slit experiment and see what happens if you keep or destroy, or look at or don't look at, the information you create by measuring what occurs at the slits themselves. WIKIMEDIA COMMONS USER PATRICK EDWIN MORAN
The thing we always have to remember, when it comes to the physical Universe, is that no matter how certain we are of our logical reasoning and our mathematical soundness, the ultimate arbiter of reality comes in the form of experimental results. When you take the experiments that we’ve performed and try to deduce the rules that govern them, you must obtain a self-consistent framework. Although there are a myriad of interpretations of quantum mechanics that are equally as successful at describing reality, none have ever disagree with the original (Copenhagen) interpretation’s predictions. Preferences for one interpretation over another — which many possess, for reasons I cannot explain — amount to nothing more than ideology.
If you wish to impose an additional, underlying set of hidden variables that truly governs reality, there’s nothing preventing you from postulating their existence. What the Kochen-Specker theorem tells us, though, is that if those variables do exist, they do not pre-determine the values revealed by experimental outcomes independently of the quantum rules we already know. This realization, known as quantum contextuality, is now a rich area of research in the field of quantum foundations, with implications for quantum computing, particularly in the realms of speeding up computations and the quest for quantum supremacy. It isn’t that hidden variables can’t exist, but rather that this theorem tells us that if you wish to invoke them, here’s what sort of finagling you have to do.
No matter how much we might dislike it, there’s a certain amount of “weirdness” inherent to quantum mechanics that we simply can’t get rid of. You might not be comfortable with the idea of a fundamentally indeterminate Universe, but the alternative interpretations, including those with hidden variables, are, in their own way, no less bizarre.
Ethan Siegal a Ph.D. astrophysicist, author, and science communicator, who professes physics and astronomy at various colleges. I have won numerous awards for science writing since 2008 for my blog, Starts With A Bang, including the award for best science blog by the Institute of Physics. My two books, Treknology: The Science of Star Trek from Tricorders to Warp Drive, Beyond the Galaxy: How humanity looked beyond our Milky Way and discovered the entire Universe, are available for purchase at Amazon. Follow me on Twitter @startswithabang

Spread the word